week 06: p-values
it all started so well
Given some observed data, it would be useful to know how surprising they are. Are these data consistent with what I'd expect by chance? If not, something more interesting might be going on.
Take Laplace's question of the birth rate of boy vs. girls in Paris, for example. He observed 251,527 boys in 493,472 births. Is this 0.51 frequency surprisingly different from what we'd expect by chance?
To be quantitative, we have to specify exactly what chance means. We formulate a hypothesis called the "null hypothesis", $H_0$, so that we can calculate $P(D \mid H_0)$, the probability distribution over different data outcomes, given the null hypothesis.
In the Laplace example, the obvious null hypothesis is that boys and girls are equiprobable: $p = 0.5$. The possible data outcomes, in $n=493472$ total births, are $c = 0 \ldots 493472$ boys. The probability of any given count of boys $c$ is a binomial distribution $P(c \mid p, n) = {n \choose c} p^c (1-p)^{n-c}$.
As Laplace was aware, the probability of any specific outcome might be absurdly small, especially as $n$ gets large. A specific outcome can be unlikely (in the sense that you wouldn't have bet on exactly that outcome beforehand), but unsurprising (in the sense that it's one of many outcomes that are consistent with the null hypothesis). If $p = 0.5$, the probability of getting exactly 50% boys ($c = 246736$) is small, 0.001. But the probability of getting a number within $\pm$ 1000 of 246736 is more than 99%. I calculated that using the binomial's cumulative distribution function in Python, which you're about to see.
Indeed, we may be able to find a range of data that are consistent with the null hypothesis, even if any particular one outcome is unlikely, and then ask if our observed data is outside that plausible range. This requires that the data can be arranged in some sort of linear order, so that it makes sense to talk about a range, and about data outside that range. That's true for our counts of boys $c$. It's also true of a wide range of "statistics" that we might calculate to summarize a dataset (for example, the mean $\bar{x}$ of a bunch of observations $x_1..x_n$).
definition of a p-value
A p-value is the probability that we would have gotten a result at least this extreme, if the null hypothesis is true.
We get the p-value from a cumulative probability function $P(X \leq x)$, so it has to make sense to calculate a CDF. There has to be an order to the data, so that "more extreme" is meaningful. Usually this means we're representing the data as a single number: either the data is itself a number ($c$, in the Laplace example), or a summary statistic like a mean.
For example, it wouldn't make sense to talk about the p-value of the result of rolling a die $n$ times. The observed data are six values $c_1..c_6$, and it's not obvious how to order them. We could calculate the p-value of observing $c_6$ sixes or more out of $n$ rolls, though. Similarly, it wouldn't make sense to talk about the p-value of a specific poker hand, but you could talk about the p-value of drawing a pair or better, because the value of a poker hand is orderable.
a p-value is a false positive rate
Recall that a false positive rate is the fraction of false positives out of all negatives: $\frac{\mathrm{FP}}{\mathrm{FP} + \mathrm{TN}}$. If we consider our test statistic $x$ to be the threshold for defining positives, i.e. everything that scores at least $x$ is called positive, then the p-value and the false positive rate are the same thing: for data samples generated by the null hypothesis (negatives), what fraction of the time do they nonetheless score $x$ or greater?
This idea leads to a simple way of calculating p-values called order statistics. Generate $N$ synthetic negative datasets for suitably large $N$, calculate your score (test statistic) for each of them, and count the fraction of times that you get $x$ or more. That's the p-value for score $x$.
Any biologist is familiar with this idea. Do negative controls. Simulate negative datasets and count how frequently a negative dataset gets a score of your threshold $x$ or more.
p-values are uniformly distributed on (0,1)
If the data actualy were generated by the null hypothesis, and you did repeated experiments, calculating a p-value for each observed data sample, you would see that the p-value is uniformly distributed. By construction, simply because it's a cumulative distribution! 5% of the time, if the null hypothesis is true, we'll get a p-value of $\leq 0.05$; 50% of the time, we'll get a p-value $\leq 0.5$.
Understanding this uniform distribution of p-values is important. Sometimes people say that a result with a p-value of 0.7 is "less significant" than a result with a p-value of 0.3, but in repeated samples from the null hypothesis, you expect to obtain the full range of possible p-values from 0..1 in a uniform distribution. Seeing a p-value of 0.7 is literally equally probable as seeing a p-value of 0.3, or 0.999, or 0.001, under the null hypothesis. Indeed, seeing a uniform distribution is a good check that you're calculating p-values correctly.
null hypothesis significance testing
P-values were introduced in the 1920's by the biologist and statistician Ronald Fisher. He intended them to be used as a tool for detecting unusual results:
"Personally, the writer prefers to set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance."
There are three important things in this passage. First, it introduced $P < 0.05$ as a standard of scientific evidence. Second, Fisher recognized that this was a "low standard". Third, by saying "rarely fails", Fisher meant it to be used in the context of repeated experiments, not a single experiment: a true effect should reproducibly and repeatedly be distinguishable from chance.
Many fields of science promptly forgot about the second two points and adopted $P<0.05$ as a hard standard of scientific evidence. A result is said to be "statistically significant" if it achieves $P < 0.05$. Sometimes, contrary to both logic and what Fisher intended, a single result with $P<0.05$ is publishable in some fields. How this travesty happened, nobody quite seems to know.
There's been many attempts at a backlash. Some people want to change the 0.05 threshold to 0.005, which rather misses the point. Some people want to ban P-values altogether.
P-values are useful, if you're using them the way Fisher intended. It is useful to know when the observed data aren't matching well to an expected null hypothesis, alerting you to the possibility that something else may be going on. But 5% is a low standard -- even if the null hypothesis is true, 5% of the time you're going to get results with $P \leq 0.05$. You want to see your unusual result reproduce consistently before you're going to believe in it.
Where you get into trouble is when you try to use a p-value as more than just a rule-of-thumb filter for potentially interesting results:
-
when you say that you've rejected the null hypothesis $H_0$, and therefore your hypothesis $H_1$ is true. A small p-value doesn't necessarily mean the data support some other hypothesis of yours, just because the data don't agree with the null hypothesis. Nothing about a p-value calculation tests any other hypothesis, other than the null hypothesis.
-
when you equate "statistical significance" with effect size. A miniscule difference can become statistically significant, given large sample sizes. The p-value is a function of both the sample size and the effect size. In a sufficiently large dataset, it is easy to get small p-values, because real data always depart from simple null hypotheses. This is often the case in large, complex biological datasets.
-
when you do multiple tests but you don't correct for it. Remember that the p-value is the probability that your test statistic would be at least this extreme if the null hypothesis is true. If you chose $\alpha = 0.05$ (the "standard" significance threshold), you're going to get values that small 5% of the time, even if the null hypothesis is true: that is, you are setting your expected false positive rate to 5%. Suppose there's nothing going on and your samples are generated by the null hypothesis. If you test one sample, you have a 5% chance of erroneously rejecting the null. But if you test a million samples, 50,000 of them will be "statistically significant".
Most importantly, using a p-value to test whether your favorite hypothesis $H_1$ is supported by the data is fundamentally illogical. A p-value test never even considers $H_1$; it only considers the null hypothesis $H_0$. "Your model is unlikely; therefore my model is right!" is just not the way logic works.
multiple testing correction
Suppose you do test $n=$ one million things. What do you need your p-value to be (per test), to decide that any positive result you get in $N$ tests is statistically significant?
Well, you expect $np$ false positives. The probability of obtaining one or more false positives is (by Poisson) $1 - e^{-np}$. This is still a p-value, but with a different meaning, conditioned on the fact that we did $n$ tests: now we're asking, what is the probability that we get result at least this extreme (at least one positive prediction), given the null hypothesis, when we do $n$ independent experiments? For small $x$, $1-e^{-x} \simeq x$, so the multiple-test-corrected p-value is approximately $np$. That is, multiply your per-test p-value by the number of tests you did to get a "corrected p-value". Like many simple ideas, this simple idea has a fancy name: it's called a Bonferroni correction. It's considered to be a very conservative correction. I'll explain one of the main reasons why in a bit.
When you report a p-value, it's important to report whether you're reporting the uncorrected one ($P(s \geq x \mid H_0)$), or a corrected one. The corrected one is a different kind of p-value.
Often, one way to make it clear without a lot of jargon is to explain how many false positives you expect in your predictions. If you say you ran a screen on $n$ samples at a threshold of $p<0.05$, I'll be looking in your paper for where you put the 5% false positive predictions that you expected: there should've been about $np$ of them. I'll feel more confident that you know what you're doing if you acknowledge that they're in your results somewhere. That is, don't talk only in terms of "statistical significance"; in large dataset analysis, you can talk in terms of the number of expected false positives. If you made 100 positive predictions, you can say "under a null hypothesis that (whatever it is), we would expect xxx of these to be false."
the empirical false discovery rate (FDR)
One reason that the Bonferroni correction is conservative is the following. Suppose you run a genome-wide screen and you make 80,000 predictions. Do you really need all of them to be "statistically significant" on their own? That is, do you really need to know that the probability of even one false positive in that search is $< 0.05$ or whatever? More reasonably, you might say you'd like to know that 99% of your 80,000 results are true positives, and 1% or less of them are false positives.
Suppose you tested a million samples to get your 80,000 positives, at a per-test p-value threshold of $< 0.05$. By the definition of the p-value you expected up to 50,000 false positives, because in the worst case, all million samples are in fact from the null hypothesis, and at a significance threshold $\alpha = 0.05$, you expect 5% of them to be called as (false) positives. So if you trust your numbers, at least 30,000 of your 80,000 predictions (80000 positives - 50000 false positives) are expected to be true positives. You could say that the expected fraction of false positives in your 80,000 positives is 50000/80000 = 62.5%.
This is called an empirical false discovery rate calculation -- specifically, (fancy names for simple ideas again) it is called the Benjamini-Hochberg FDR.
Recall that the false discovery rate (FDR) is the proportion of your called "positives" that are false positives: FP / FP + TP. If all we have is the p-value $p$, we can estimate the expected number of false positives if we know what fraction of our $n$ samples are negative versus positive -- but we don't. Moreover, we don't know the number of true positives, because the p-value doesn't say anything that. What the Benjamini-Hochberg empirical FDR is doing is approximating a worst-case bound: assume that all $n$ of the samples are negatives, thus estimate that FP = $np$, and calculate FP / total called positives. It's an approximation that's most accurate when all or almost all of the $n$ samples are negatives, and the inferred TP is negligibly small compared to $n$.
what Bayes says about p-values
A good way to see the issues with using p-values for hypothesis testing is to look at a Bayesian posterior probability calculation. Suppose we're testing our favorite hypothesis $H_1$ against a null hypothesis $H_0$, and we've collected some data $D$. What's the probability that $H_1$ is true? That's its posterior:
$$ P(H_1 \mid D) = \frac{ P(D \mid H_1) P(H_1) } { P(D \mid H_1) P(H_1) + P(D \mid H_0) P(H_0) } $$
To put numbers into this, we need to be able to calculate the likelihoods $P(D \mid H_1)$ and $P(D \mid H_0)$, and we need to know how the priors $P(H_0)$ and $P(H_1)$ -- how likely $H_0$ and $H_1$ were before the data arrived.
What does p-value testing give us? It gives us $P( s(D) \geq x \mid H_0)$: the cumulative probability that some statistic of the data $s(D)$ has a value at least as extreme as $x$, under the null hypothesis.
So we don't know anything about how likely the data are under our hypothesis $H_1$. We don't know how likely $H_0$ or $H_1$ were in the first place. And we don't even know $P(D \mid H_0)$, really, because all we know is a related cumulative probability function of $H_0$ and the data.
Therefore, in general, it is utterly impossible to calculate a Bayesian posterior probability, given a p-value. A p-value simply cannot tell you how much evidence your data give in support of your hypothesis $H_1$.
(This is the fancy way of saying that just because the data are unlikely given $H_0$ does not logically mean that $H_1$ must be true.)
what Nature (2014) said about p-values
The journal Nature ran a commentary article in 2014 called "Statistical errors", about the fallacies of p-value testing. The article showed one figure, reproduced to the right. The figure shows how a p-value corresponds to a Bayesian posterior probability, under three different assumptions of the prior odds, for $P=0.05$ or $P=0.01$. It shows, for example, a result of $P=0.01$ might be "very significant", but the posterior probability of the null hypothesis might still be quite high: 30%, if the null hypothesis was pretty likely to be true to begin with. The commentary was trying to illustrate the point that the p-value is not a posterior probability, and that a "significant" p-value does not move the evidence as much as you might guess.
Figure from Nuzzo, "Statistical errors", Nature (2014), showing
how a P-value affects a posterior probability.
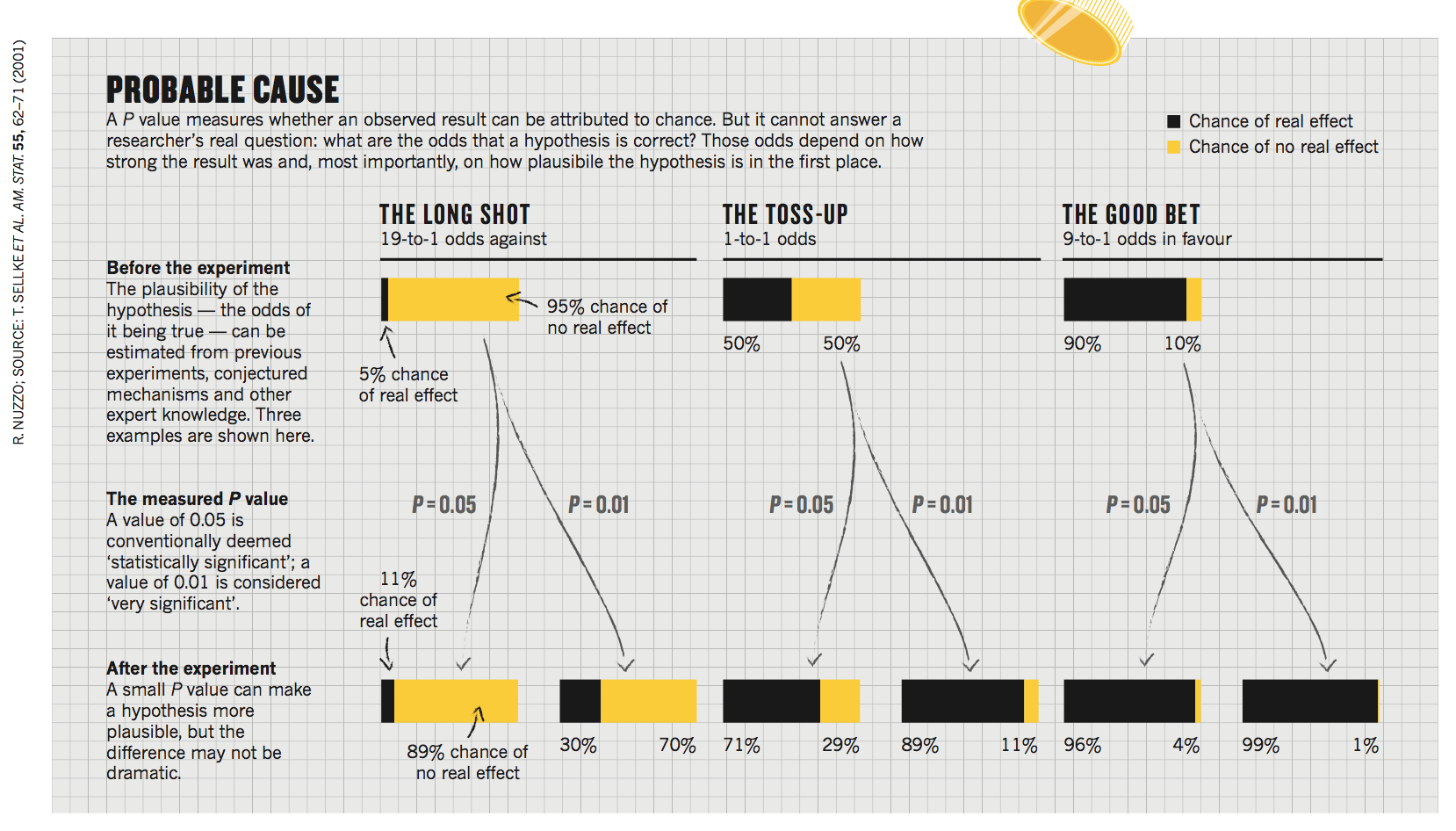
But hang on. I just finished telling you that it is utterly impossible (in general) to calculate a posterior probability from a p-value, and here we have Nature doing exactly that. What's going on? The p-value literature is often like this: many righteous voices declaiming what's wrong with p-values, while making things even more confusing by leaving out important details and/or making subtle errors. Which means I'm probably doing the same thing, even as I try not to.
The key detail in the Nature commentary flashes by in a phrase -- "According to one widely used calculation...", and references a 2001 paper from statistican Steven Goodman. Let's look at that calculation and see if we can understand it, and if we agree with its premises.
First we need some background information on statistical tests involving Gaussian distributions.
Gaussian distributions
A Gaussian probability density function is defined as: And where's this come from? Magic? Turns out that we can derive the Gaussian from first principles with a little calculus, if we assume we seek the least informative -- i.e. maximum entropy -- distribution that is constrained to have some mean $\mu$ and variance $\sigma^2$. If instead we only constrain to a mean $\mu$, we derive the exponential distribution. We'll leave this aside, and maybe get back to it someday, since it's fun to see.
$$ P(x \mid \mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x - \mu)^2}{2 \sigma^2}} $$
A useful thing to notice about Gaussian distributions is that they're identical under a translation of $x$ and $\mu$, and under a multiplicative rescaling of $\sigma$. The probability only depends on the ratio $(x - \mu) / \sigma$: that is, on the number of standard deviations away from the parametric mean. So, if I calculate a so-called Z-score:
$$ Z = \frac{x - \mu} {\sigma} $$
then I can talk in terms of a simplified standard normal distribution:
$$ P(Z) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{Z^2}{2}} $$
This is a very useful simplification - among other things, it'll be easier to remember things in units of "number of standard deviations away from the mean", and will help you develop general, quantitative intuition for Gaussian-distributed quantities.
The probability that we get a Z score at least as extreme as $z$ is an example of a p-value:
$$ P(Z \geq z) = \int_z^{\infty} P(Z) $$
We might be interested not just in whether our observed statistic $x$ is surprisingly larger than $\mu$, but also if it's surprisingly smaller. That's the difference between what statisticians call a "one-tailed" test versus a "two-tailed" test. In a one-tailed test, I'm specifically testing whether $P(Z \geq z)$, for example; in a two-tailed test, I'm testing the absolute value, $P(|Z| \geq z)$. The Gaussian is symmetric, so $P(|Z| \geq z) = P(Z \leq -z) + P(Z \geq z) = 2 P(Z \geq z)$.
We get $P(Z \geq z)$ from the Gaussian cumulative distribution function (CDF):
$$ P(Z \geq z) = 1 - P(Z < z) = 1 - \mathrm{CDF}(z) $$
(Because this is a continuous function, $P(Z < z) = P(Z \leq z)$ asymptotically; there's asymptotically zero mass exactly at $P(Z = z)$.)
There's no analytical expression for a Gaussian CDF, but it can be
computed numerically. In Python, the scipy.stats.norm module
includes a CDF method and more:
import scipy.stats as stats
z = 1.96
1 - stats.norm.cdf(z) # gives one-tailed p-value P(Z >= 1.96) = 0.025
stats.norm.sf(z) # 1-CDF(x) is the "survival function"; more numerically stable
p = 0.05 # you can invert the survival function with `.isf()`:
stats.norm.isf(p) # given a 1-tailed p-value P(Z > z), what Z do you need? (gives 1.64)
stats.norm.isf(p/2) # or for a two-tailed P(|Z| > z) (gives 1.96)
Now we've got some background (and Python), back to the calculation from Goodman that the Nature commentary is based on.
back to Goodman's calculation
To get the Bayesian posterior, we'll need the likelihood $P(Z \mid H_0)$ as a probability density function, but we've got a p-value, which is a cumulative distribution.
Crucially, for a Gaussian-distributed statistic, if I tell you the p-value, you can calculate the Z-score (by inverting the CDF); and given the Z-score, you can calculate the likelihood $P(Z)$. Thus in this case we can convert a P-value to a likelihood of the null hypothesis for a $Z$-score:
$$ P(Z \mid H_0) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{Z^2}{2}} $$
For example, a p-value of $P = 0.05$ for a two tailed test $P(|Z| > z)$ implies Z = 1.96, by inverting the CDF. Roughly speaking, 5% of the time, we expect a result more than 2 standard deviations away from the mean on either side.
So now we've got the likelihood $P(Z \mid H_0)$. That's one of our missing terms dealt with, in the Bayesian posterior probability calculation. How about $P(Z \mid H_1)$? Well, that's the tricksy one.
Observe that the best possible hypothesis $H_1$ is that its mean $\mu$ happens to be exactly on the observed statistic $x$. If so, then $x - \mu = 0$, thus $Z = 0$, so:
$$ P(Z \mid H_1) \leq \frac{1}{\sqrt{2 \pi}} $$
It's absolutely cheating to choose $x$ as the mean for our $H_1$ after we've looked at the data $x$. That's why this is an upper bound, being as favorable to $H_1$ as you could possibly be. It would be more correct to look at a range of possible $\mu_1$ values for $H_1$, with an explicit prior distribution. We'll come back to this.
Now we can calculate a bound on the likelihood odds ratio, the so-called "Bayes factor" for the support for the null hypothesis:
$$ \frac{P(Z \mid H_0)} {P(Z \mid H_1)} \geq e^{-\frac{Z^2}{2}} $$
The "Bayes factor" represents how much the relative odds in favor of the null hypothesis changes after we observed the data.
We still need to deal with the prior probabilities $P(H_0)$ and $P(H_1)$. Recall that we can rearrange the posterior in terms of the Bayes factor and the prior odds:
$$ P(H_0 \mid Z) = \frac{P(Z \mid H_0) P(H_0)} {P(Z \mid H_0) P(H_0) + P(Z \mid H_1) P(H_1)} = \frac { \frac{P(Z \mid H_0) P(H_0)} {P(Z \mid H_1) P(H_1)} } { \frac{P(Z \mid H_0) P(H_0)} {P(Z \mid H_1) P(H_1)} + 1} = \frac { \frac{P(Z \mid H_0) } { P(Z \mid H_1)} } { \frac{P(Z \mid H_0) } { P(Z \mid H_1)} + \frac{P(H_1)}{P(H_0)}} $$
Since we have a lower bound on the Bayes factor, we're also going to get a lower bound on the posterior probability of the null hypothesis.
Now we're ready to plug numbers in, to see what Goodman is doing.
Suppose $H_1$ and $H_0$ are 50:50 equiprobable a priori, and you observe a mean $Z$ that is $Z=1.96$ standard deviations away from the null hypothesis' $\mu$. The two-tailed P-value is 0.05. The minimum Bayes factor is $e^{-\frac{Z^2}{2}} = 0.15$. The posterior probability of the null hypothesis is no less than $\frac{0.15} {0.15 + 1} = 13$%. Obtaining our "significant" P-value of 0.05 only moved our confidence in the null hypothesis from 50% to 13%.
Now suppose that the null hypothesis is more likely a priori, with prior probability 95%. (In many biological experiments, we're usually going to observe unsurprising, expected results.) Now the posterior probability of the null is $\frac{0.15} {0.15 + \frac{0.05}{0.95}} = 74$%. Our "significant" P-value hardly means a thing -- it's still 74% probable that the null hypothesis is true. If this is how we did science -- if we published all our "statistically significant" results, with only the p-value as evidence -- 74% of our papers would be wrong.
This is the gist of it. The numbers in Nuzzo's 2014 Nature commentary are actually based on a calculation that's a step more sophisticated than this. Instead of saying that $H_1$ has exactly $\mu = Z$ (which, as we said, is somewhat bogus, choosing your hypothesis to test after looking at the data), you can do a version of the calculation where you say that any $\mu_1$ is possible for $H_1$, with a prior distribution symmetrically decreasing around $\mu_0$. Under this calculation, the probability $P(Z \mid H_1)$ is lower, so the bound on the Bayes factor is higher -- so the posterior probability of the null hypothesis is decreased even less, for a given p-value. Thus Nuzzo's figure says "29% chance of no real effect" for the p=0.05/50:50 case and "89% chance of no real effect" for the p=0.05/95:5 case, instead of the 13% and 74% I just calculated. Table 1 in the Goodman paper shows both variants of the calculation, for a range of p-values.
summary
Thus the exact numbers in Nuzzo's 2014 Nature commentary turn out to depend on very specific assumptions -- primarily, that the p-value comes from a hypothesis test where we're asking if a Gaussian-distributed mean is different from an expected value. There are many other situations in which we would use p-values and hypothesis testing. It is indeed true that in general you cannot convert a p-value to a Bayesian posterior probability.
But Goodman's and Nuzzo's arguments are "directionally correct", as we say in politics these days, and it is useful to see a worked numerical example. A "significant" or even a "highly significant" p-value does does not mean that the null hypothesis has been disproven -- it can easily remain more probable than the alternative hypothesis.
further reading
-
Regina Nuzzo, Statistical errors, Nature, 2014.
-
Steven Goodman, A dirty dozen: twelve p-value misconceptions, Seminars in Hematology, 2001.
-
Steven Goodman, Of p-values and Bayes: a modest proposal, Epidemiology, 2001.