Phylogenetic trees

Notes by Jenya Belousova (2024)

Introduction

Tree as a formalization of evolutionary process

What is a tree from a mathematical point of view? First of all, it is a graph, meaning that it has vertices and paths. But not any graph can be a tree, specifically, only connected (there's no isolated vertices), acyclic (there's no loops), undirected (paths don't have a direction) graph. However, this definition embeds more trees than we are interested in as phylogeneticists. Phylogenetic trees are thought to be binary.

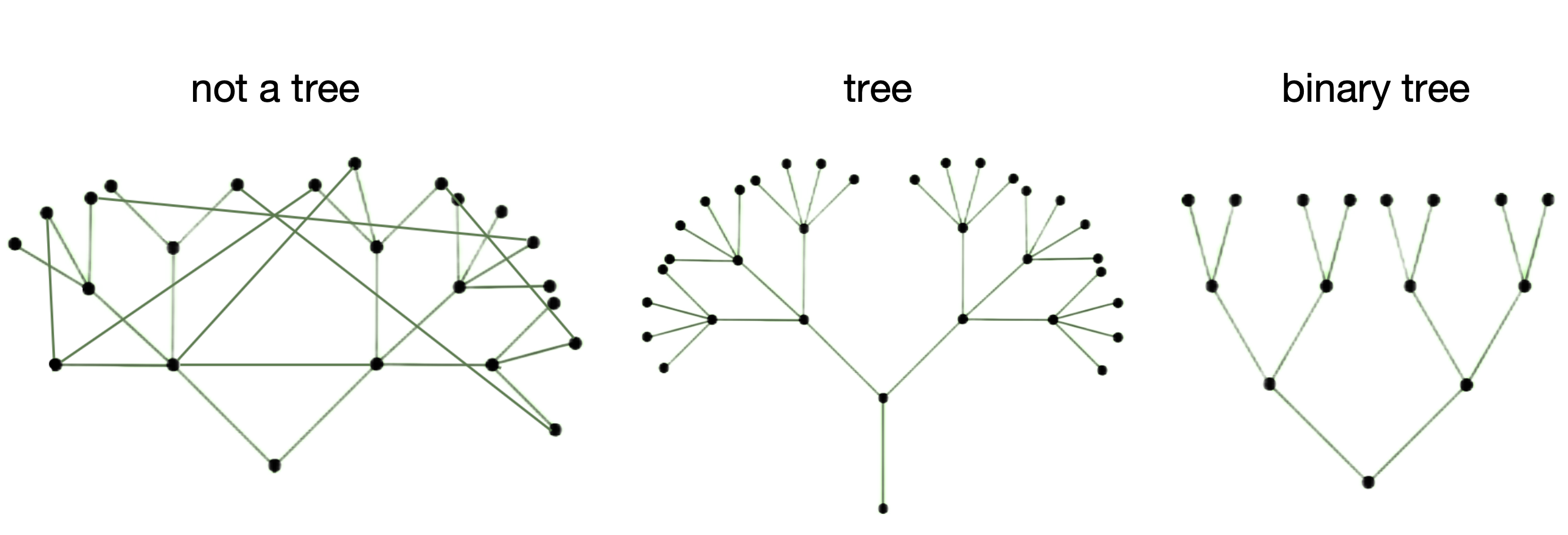
Graph examples.
First graph contains cycles, therefore, it is not a tree, second graph is a tree containing trichotomies, last graph is a binary tree.

So, the most common mathematical object used to formalize evolutionary tree is a binary tree graph. However, some parts of this definition are constantly tweaked by biology.

1) Can you think of an evolutionary tree containing some kind of cycle?

2) Can an evolutionary tree be not binary?

These are the questions for us to think about.

Rooting problem

3) If I give you 5 species: mouse, cat, lion, human, rat, chimp; can you make a tree for these species "empirically", based on your basic knowledge?

Seems easy! Until it gets harder...

Algorithms in details

Now let us go into details on two last algorithms discussed in the lecture: parsimony and maximum likelihood.

Parsimony, Fitch algorithm

Let us consider a tiny alignment of four sequences with three sites. There are three possible tree topologies in this case. We need to find a tree with the minimal number of evolutionary events (nucleotide substitutions in our case) required to happen for our alignment. We will look at each site separately for a given tree and count the number of substitutions (red marks on the picture). If the clade with two leaves has the same nucleotide, then the substitution happened upstream this clade.


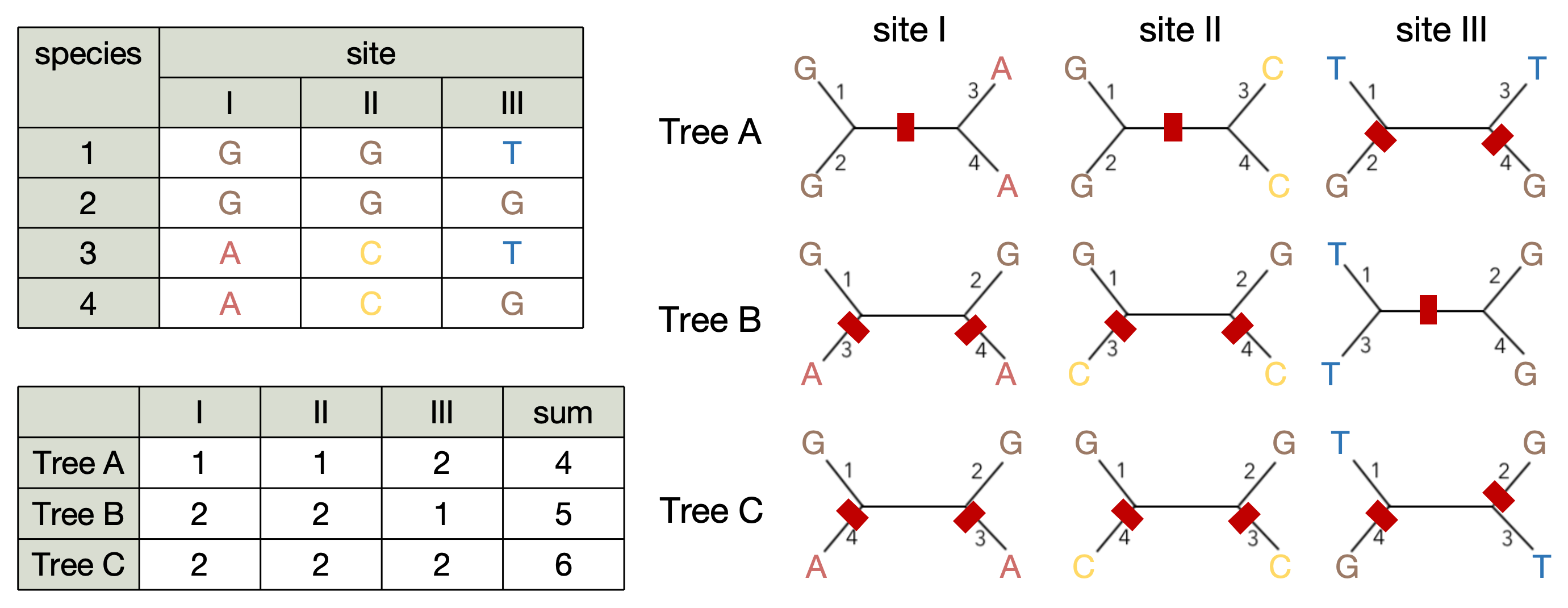
Fitch parsimony algorithm.



First aligned column is GGAA, second - GGCC, third - TGTG. There are three possible tree topologies in this case (A - when 1, 2 and 3, 4 converge first; B - when 1, 3 and 2, 4 converge first; C - when 1, 4 and 2, 3 converge first). Therefore, the total number of required substitutions for ((1,2)(3,4)) tree is 4; for ((1,3)(2,4)) tree is 5; for ((1,4)(2,3)) tree is 6.

Tree A wins! Note, that in Fitch algorithm each substitution adds cost of 1 to the total cost of the tree.

Weighted parsimony and Maximum likelihood

are covered right here w13-section.ipynb. To display the explanatory pictures, please also download them (one more) in the same directory as the w13-section.ipynb jupyter notebook.