homework 13: the adventure of the three trees
Your time in the Holmes lab is nearing its end. Both you and Moriarty are interviewing for the same position in Irene Adler's lab at the University of Bohemia. Holmes has always highly recommended her lab.
Adler works on phylogenetic inference methods. She has an unusually substantive interview procedure. She draws you and Moriarty a picture of three alternative trees for four taxa:
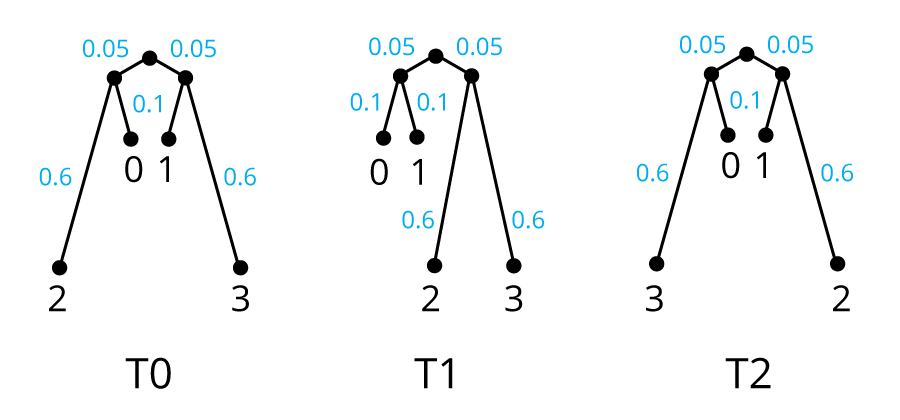 Adler's three trees. There are three possible unrooted topologies for a
tree of n=4 taxa. T0 joins taxa (0,2) and (1,3) as closest neighbors;
T1 joins (0,1) and (2,3); T2 joins (0,3) and (1,2).
For the purpose of simulating sequences down the tree from a common ancestor,
the three trees are
rooted arbitrarily at the midpoint of the central branch that joins
two pairs of taxa. The branch length to taxa 0 and 1 from their
internal node is 0.1 substitutions/site on all three trees; the branch
length to taxa 2 and 3 is 0.6; and the distance from the root to each
internal node is 0.05.
Adler's three trees. There are three possible unrooted topologies for a
tree of n=4 taxa. T0 joins taxa (0,2) and (1,3) as closest neighbors;
T1 joins (0,1) and (2,3); T2 joins (0,3) and (1,2).
For the purpose of simulating sequences down the tree from a common ancestor,
the three trees are
rooted arbitrarily at the midpoint of the central branch that joins
two pairs of taxa. The branch length to taxa 0 and 1 from their
internal node is 0.1 substitutions/site on all three trees; the branch
length to taxa 2 and 3 is 0.6; and the distance from the root to each
internal node is 0.05.
She says, suppose T0 is the true tree. We sample a random sequence of some chosen length $L$ at the root, and then generate simulated sequences down the tree, using a simple Jukes-Cantor substitution model, with branch lengths (in substitutions/site) as shown. This results in a simulated ungapped multiple sequence alignment of 4 leaf taxa and 3 ancestral sequences. Now we take the simulated MSA of the four sequences at the leaves and we do inference with four methods: (1) UPGMA, using pairwise distances inferred by the same Jukes-Cantor model; (2) neighbor-joining, using those same pairwise distances; (3) parsimony; and (4) maximum likelihood, again using the Jukes-Cantor model.
She asks, what will happen? Which method(s) will tend to infer which of the three trees is correct (i.e. T0, which was actually used to simulate the data, as opposed to T1 or T2), and moreover will get more accurate in its inference as the amount of data (the alignment length $L$) increases? Conversely, which method(s) will tend to infer the incorrect tree?
Moriarty says, he would just use parsimony, because it's assumption-free, so obviously it's the best method. He goes off to book a business-class flight to Bohemia.
You're not so sure. You look at those long branches to taxa 2 and 3 and recognize that this little example might be crafted as a compact demonstration of the strengths and weaknesses of the different main types of tree inference methods. It seems worthwhile to actually do the experiment that Adler proposed.
1. Implement code for simulating sequences down tree T0.
Using a Jukes-Cantor DNA substitution model, write a function that generates sequences down tree T0, for a given alignment length $L$.
In more detail: have your function generate a random (i.i.d., uniform composition) DNA sequence of length $L$ at the root. Then, following tree T0's branching pattern, generate each descendant sequence from its ancestor, using its given branch length (in substitutions/site) to parameterize a Jukes/Cantor $P(b \mid a,t)$ for the probability of obtaining descendant residue $b$ from ancestral residue $a$ in time $t$. The result is an ungapped multiple sequence alignment of the four sequences (0-3) at the leaves of the tree. Recall that in a Jukes-Cantor substitution model, the expected number of substitutions/site along a branch is 3$\alpha t$, so to convert a branch length $b_i$ to what you need for calculating Jukes-Cantor, $\alpha t_i = b_i / 3$.
You also get the sequences at the ancestral nodes. Your function can keep those too if you want, but you won't use them in what follows. For testing phylogenetic inference, we'll now pretend that we only observe the synthetic sequences at the leaves.
Recognize that we needed to choose a root to generate sequences down a tree, but since we are using a reversible substitution matrix, the placement of the root actually has no effect on the probability distribution of sequences at the leaves. In what follows below, we will choose a best tree T0|T1|T2 based on their inferred unrooted topologies. If you don't believe that the position of the root doesn't matter to parsimony or to ML with a reversible substitution process, you'll be able to see for yourself. When you have your parsimony and ML implementations below, you could vary where you put the root on the three trees, and test that the 5 possible rooted topologies for each unrooted tree T0,T1,T2 all give you the same parsimony cost and Jukes-Cantor log likelihood.
2. Implement the first step of UPGMA to choose a best tree
Write a function to calculate a 4x4 pairwise distance matrix $d_{ij}$ for all pairs (i,j) of sequences 0-3, using Jukes-Cantor distances.
Then write a mini UPGMA function that takes that distance matrix and identifies which (i,j) pair would be joined first by the UPGMA algorithm, then uses that (i,j) pair to determine which of the three tree topologies would be chosen (based on their unrooted topologies).
I'm writing the problem this way to save you from having to implement the bookkeeping for a complete UPGMA or NJ implementation that iteratively builds up an inferred tree with its branch lengths. This way, you only have to look at the $d_{ij}$ pairwise distances (either directly, for UPGMA, or via the $D_{ij} = d_{ij} - (r_i + r_j)$ equation for NJ) to determine the best tree. Some more explanation: for just n=4 taxa, you don't need to implement all of UPGMA, or any other distance-based method, to know which of these three (unrooted) tree topologies it will choose. All you need to do is one iteration: choose the first pair (i,j) to join. For example, if the algorithm chooses to join pair (0,1) first, then it must result in the unrooted topology corresponding to T1. If the algorithm chooses to join pair (1,3) first, then it must result in the unrooted topology for T0.
UPGMA of course infers a rooted tree, not an unrooted one. But for our
purposes, choosing the best tree from the first joined pair (i,j) is
sufficient for the point we're testing. Since UPGMA infers an
ultrametric tree, with all leaf taxa equidistant from the root, we
already know that UPGMA can't correctly infer the true branch lengths
on any these three trees, which are additive but not ultrametric.
It's possible to get more than one (i,j) pair with the same minimum
distance. In my code, I went to the trouble of choosing randomly among
equally optimal (i,j) in such cases. If you simply use np.argmin(), it'll give you
the first (lowest-indexed) optimal (i,j) in the distance matrix, which
will introduce some bias into which tree is chosen. Another way you
can handle this is to not infer any best tree if there are ties.
The same issue with ties arises in parsimony and ML, too.
3. Implement the first step of Neighbor-Joining
Using your $d_{ij}$ distance matrix from above, write a mini NJ function that takes that distance matrix and does the first step of neighbor-joining to choose the first (i,j) pair to be joined as neighbors. Use that (i,j) pair to return which of the three tree topologies is favored by NJ.
4. Implement Fitch parsimony
Write a function that takes a tree topology and a multiple sequence alignment as input, and uses the Fitch parsimony algorithm to calculate the minimum cost (in total substitutions) of the tree.
To choose a best tree, you'll run this function on each of the three trees, and choose the one with minimum Fitch parsimony cost.
5. Implement maximum likelihood
Write a function that takes a tree topology, branch lengths (in substitutions/site) and a multiple sequence alignment as input, and uses the Felsenstein peeling algorithm to calculate the log likelihood of the tree, using a Jukes-Cantor substitution model.
A real implementation of ML tree inference has to optimize branch lengths for each unrooted topology. Here, we're using the given branch lengths, which considerably simplifies things. To choose a best tree, you'l run this function on each of the three trees, and choose the one with maximum log likelihood.
6. Do Adler's experiment
Generate 100 simulated alignments, from tree T0, for each of four different alignment lengths L=(20, 100, 500, 2000). (That's 400 simulated alignments in all.) For each alignment, find the best tree favored by each of the four methods: mini UPGMA, mini NJ, parsimony, and ML.
For each method, output a table that shows how many of the 100 simulations result in inferring tree T0 vs. T1 vs. T2, for the various choices of L.
Which method(s) accurately infer that T0 is the true tree (the tree that was used to simulate the data), with the inference becoming more accurate as $L$ increases?
Which method(s) become increasingly inaccurate, converging to an inaccurate tree inference as $L$ increases? For each inaccurate method, provide an explanation for why it's being inaccurate.
allowed modules
I only needed NumPy for this:
import numpy as np
But you're also free to use any of the modules we've used in the semester: NumPy, Matplotlib, Pandas, Seaborn, SciPy's stats, special, and optimize modules, and re.
turning in your work
Submit your Jupyter notebook page (a .ipynb file) to
the course Canvas page under the Assignments
tab.
Name your
file <LastName><FirstName>_<psetnumber>.ipynb; for example,
mine would be EddySean_13.ipynb.
We grade your psets as if they're lab reports. The quality of your text explanations of what you're doing (and why) are just as important as getting your code to work. We want to see you discuss both your analysis code and your biological interpretations.
Don't change the names of any of the input files you download, because the TFs (who are grading your notebook files) have those files in their working directory. Your notebook won't run if you change the input file names.
Remember to include a watermark command at the end of your notebook,
so we know what versions of modules you used. For example,
%load_ext watermark
%watermark -v -m -p jupyter,numpy,matplotlib