pset 04: the adventure of the erratic nucleotide

Your lab is using CRISPR spacer sequences to identify which SEA-PHAGE phages infect which bacterial hosts. The idea is to sequence CRISPR spacers, then computationally match those short host sequences ($\sim$30-40nt) to SEA-PHAGE genome sequences. Matches suggest that this host was infected by this phage at some point.

Moriarty's erratic DNA sequencer

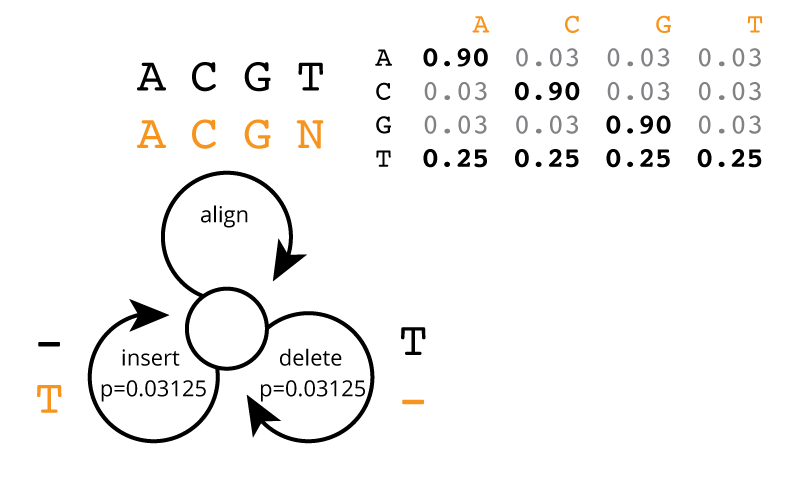
Moriarty is leading the project. He is using his latest invention, a new DNA sequencing machine that's faster and cheaper than any other existing technology. Unfortunately, his technology also has a peculiar error profile: it cannot sequence T's accurately. A, C, and G nucleotides are sequenced with 90% accuracy, but T positions are called uniformly randomly, 25% each base. Worse, T's are inserted (into the observed read) randomly 3.125% of the time (that's 1/32), and T's are deleted (from the actual sequence) 3.125% of the time.

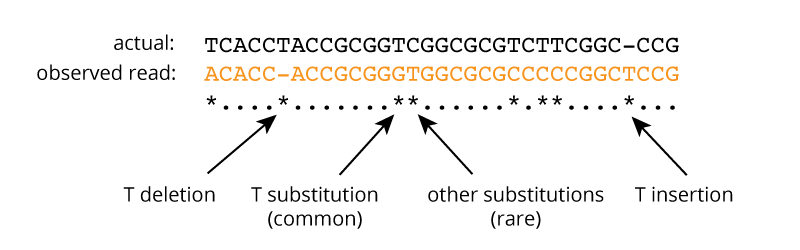
An example of a Moriarty read (in orange) aligned to the actual corresponding 32nt CRISPR spacer sequence is shown below. 8 asterisks mark the positions of basecalling errors: 1 T deletion, 1 T insertion, 5 T substitutions, and 1 substitution at another base (here, a C).

Figure showing an example alignment of one 32nt CRISPR spacer to a Moriarty sequencing read, as described above in the text.

This error process is illustrated as a state machine in the figure below. The state machine consumes symbols from the actual sequence (black symbols) and generates symbols on the observed read. Each step of the machine, it follows one of the three arrows. At any step, it can insert a T with probability 1/32 (0.03125); at any T residue in the actual sequence, it can delete that T with probability 1/32; else, it generates a base aligned to the actual base, with probabilities as shown in the table: 90% accuracy for A|C|G, and uniformly random 25% for basecalling a T.

Figure showing the state machine model with probabilities for generating insertions, deletions, and substitutions in an observed read from an actual spacer sequence.

Unfortunately, these basecalling errors seem to make Moriarty's reads useless. He has been unable to computationally map spacer reads to phage genomes, even using positive controls of known host-phage interactions and well-studied host CRISPR arrays. It's not hard to understand why it's failing. The expected identity of an ungapped alignment between a read and its source spacer (assuming uniform 25% each base) is only 74% (90% at 75% of the bases + 25% at 25% of the bases), and the insertions and deletions just make things worse. Standard read mapping methods assume at most one or two mismatches, and even homology search methods like BLAST and HMMER fail to resolve signal from noise on short sequence comparisons that are this divergent.

But here's where you come in. Even just a few weeks into MCB112, you know enough to make a customized alignment model, specific to Moriarty's error profile. You know that a custom alignment substitution matrix $\sigma(b|a)$ can be derived as $\log_2 \frac{p(b|a)}{f(b)}$, and thus (assuming uniform 25% base composition), you derive the alignment scores that should be used. Using what you've learned this week in MCB112, you sketch the following alignment score model at a white board, mirroring the generative probability model:

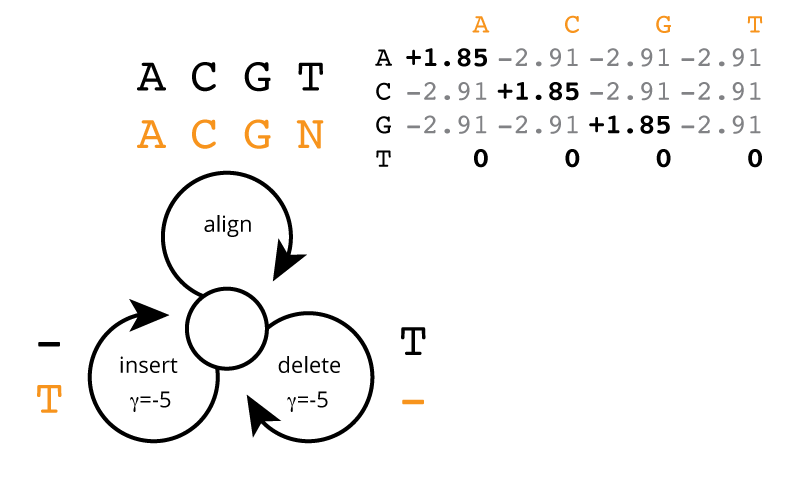
Figure showing the state machine model and log-likelihood-ratio scores for aligning Moriarty's reads to a source sequence, with +1.85 bits for each identical A|C|G alignment, -2.91 bits for each mismatch to an actual A|C|G, and 0 bits for alignments to a T in the actual sequence.

One thing you don't know from MCB112 yet is how to set the gap cost for insertion/deletion. You schedule a 60-second meeting with your professor, Holmes. Professor Holmes takes one glance at the insertion/deletion probability of 1/32 and says it's elementary: $\log_2 \frac{1}{32}$ = -5, so your gap score should be -5. He also mutters something about missing a parameter if you were really doing this precisely right, but since we haven't seen hidden Markov models yet, he can't explain it to you. You have no idea how he did this, but whatever; you put in a -5 for the insertion/deletion score in the alignment model. You can verify (in section 2 below) that it's a reasonable choice.

1. implement this global alignment model

Hint: the optimal global alignment score for the sequences in the example figure above, for actual sequence TCACCTACCGCGGTCGGCGCGTCTTCGGCCCG and observed read ACACCACCGCGGGTGGCGCGCCCCCGGCTCCG, is 33.34 bits: 25 identical aligned A|C|G residues x 1.85 + 1 mismatch A|C|G alignment x -2.91 + 5 aligned T residues x 0 + 1 T deletion x -5 + 1 T insertion x -5 = 33.34. This gives you a known test case to try, and you can make others. I put the two sequences there so you can cut&paste them, since you can't do that from the figure.

Write a function to perform global sequence alignment between two sequences, the actual sequence and a read sequence, by dynamic programming, using the scoring model above.

Have your function take a gap score as an argument, because we're going to vary it in the next section.

Your function can also take a match score (for identical A|C|G aligned pairs) and a mismatch score (for mismatches involving A|C|G on the actual sequence), but we won't be varying them, so you can also just hardcode them if you prefer.

Have your function return the optimal global alignment score.

You do not need to find the optimal alignment itself (you don't need to implement the traceback phase of the dynamic programming, only the matrix fill phase).

2. check that the -5 gap score seems reasonable

You're not quite sure how Professor Holmes immediately stated that -5 was a good choice for gap score. Classically, gap scores are arbitrary parameters that have to be set empirically. One way to do this is to run a simulation where we score a bunch of positive control sequences, and a bunch of negative control sequences, and calculate the difference between mean positive and negative scores. We can then vary the gap score and optimize for the biggest gap, which should give us the best chance of discriminating positives from negatives.

Write a function that takes an actual sequence as input, and uses the probabilistic error model to generate a simulated read from it.

Use that function for generate positive control pairs, by making random (i.i.d., uniform base composition) 32nt "actual sequences" and sampling a read from each one.

Generate negative control pairs by generating two random i.i.d. 32nt sequences.

This is computationally expensive. My version took about 5-10 minutes to run in total, over all the gap choices. Otherwise I would have done more than 2000 samples each, to sharpen up my estimates of these means. For each gap score choice in [ 0, -2, -4, -5, -6, -8, -10 ], collect scores for 2000 positive and 2000 negative simulated pairs; calculate the difference between the means.

Does -5 look like a reasonable choice? Why? Of course it does. Would Holmes lead you astray?

3. implement the alignment model for genome scanning

Hint: the recursion is the same. The only modifications you need are in initialization and termination steps of the DP algorithm. Now write a new dynamic programming function that modifies your global alignment routine to do global/local alignment: global with respect to the read, local with respect to the actual sequence. Using global/local ("glocal") alignment, you can find matches in a target genome sequence that you require to align to the entire query read sequence, not just part of it.

Have this function return the best score found in the target sequence, and the end position where that best score was found.

You don't need to find the start position of the best alignment, only the end. Finding the start as well would require a traceback phase to your dynamic programming, and I'm sparing you that.

4. demonstrate proof of principle

Moriarty doesn't believe your algorithm works, because he didn't think of it. He challenges you with an example read GCAGCGGAGGAACCAGACATACTGACGAGCCGT and three SEA-PHAGE genomes Citius, TPA4, and Vulture. He happens to know which of the three phage genomes this CRISPR spacer sequence is targeting (and thus where a match is expected), and he bets you a bag of donuts you can't figure out which one.

Download the example read and those genomes either by right-clicking the links above, or with wget or curl, e.g.:

wget http://mcb112.org/w04/example_read.fa
wget http://mcb112.org/w04/Citius
wget http://mcb112.org/w04/TPA4
wget http://mcb112.org/w04/Vulture

(They are in FASTA format. You'll need a FASTA parsing function. You wrote one for pset 01.)

Search each genome with the GCAGCGGAGGAACCAGACATACTGACGAGCCGT read, finding the best score and position in each of the three genomes.

Again, computationally intensive. My scans took about 1-2 minutes per genome. I would have done this for more reads, but it would take too long. Python is slow! I would guess a C implementation of this is at least 10x faster, and maybe 100x. Which genome did this read come from?

allowed modules

NumPy, Matplotlib, Pandas, Seaborn.

You really only need NumPy for this.

You don't need to make any plots, but you can, so I included Matplotlib and Seaborn. You also don't need any Pandas data frames, but you can if you want to (like, in collecting a data table for the gap parameter sweep part).

import numpy as np
import matplotlib.pyplot as plt     # optional
import pandas as pd                 # optional
import seaborn as sns               # optional

%matplotlib inline

turning in your work

Submit your Jupyter notebook page (a .ipynb file) to the course Canvas page under the Assignments tab. Name your file <LastName><FirstName>_<psetnumber>.ipynb; for example, mine would be EddySean_04.ipynb.

We grade your psets as if they're lab reports. The quality of your text explanations of what you're doing (and why) are just as important as getting your code to work. We want to see you discuss both your analysis code and your biological interpretations.