week 09: mixed feelings

single-cell RNA-seq data

Starting around around 2009 people started doing RNA-seq experiments on single cells (scRNA-seq). The technologies for doing scRNA-seq experiments continues to advance rapidly.

Single cell RNA-seq was a breakthrough. It allows us to see cell-to-cell heterogeneity in transcriptional profiles, including different cell types. So long as we're willing to use transcriptional profile as a proxy for "cell type", by using single-cell RNA-seq we can comprehensively survey all the cell types present in some tissue. This is especially powerful in understanding complex biological structures composed of many cell types, like brains. Single cell RNA-seq can even be applied to single bacterial cells.

A single-cell RNA-seq data set typically consists of a 2D $N \times G$ matrix of $N$ cells by $G$ genes. Each entry $y_{ig}$ is a mapped read count, the number of sequencing reads from cell $i$ that mapped to gene $g$. To get to the $y_{ig}$ matrix, there is a bunch of important pre-processing of the sequencing read data, followed by computationally mapping reads to the transcriptome (or genome). If you're interested, a (slightly aging) review of the experimental design, analysis, and interpretation of single-cell RNA-seq experiment is [Stegle, Teichmann, and Marioni, 2015].

These counts are typically small, often on the order of 0-100 mapped reads per gene. That makes sense, because the actual number of mRNA molecules per gene in a cell is on that same order too. Only highly expressed genes are detected reliably. Low-level transcripts may not be sampled at all. Many $y_{ig}$ are zeros. Some scRNA-seq analysis methods assume that there are more zeros than expected from just sampling noise, and they add extra machinery to handle what's called "dropout".

Thus scRNA-seq experiments typically detect expression of fewer genes than population RNA-seq experiments do, with less accuracy in quantitating expression levels. Population ("bulk") RNA-seq experiments are better at deeply sampling the transcriptome of a population of cells. Single cell experiments are most useful for identifying enough higher-expressed genes to distinguish useful cell types. Highly-expressed genes that are useful for distinguishing cell types are often called "marker genes". Some cell types are still often operationally identified by a single marker gene they express highly, such as the parvalbumin-positive (Pv+) interneurons in mammalian hippocampus.

It is more common these days to distinguish cell types by clustering cells in an scRNA-seq data set according to how close their transcriptional profiles (their count vectors $y_i$) are.

One can pool single cell data after clustering to approximate population RNA-seq on purified cell type populations, although the higher technical difficulty of single cell RNA-seq experiments probably makes this an imperfect approximation, with higher technical noise. This is called "pseudo-bulking".

Thus, cluster inference methods are super important in scRNA-seq analyses. We want to cluster transcriptional profiles of single cells in our data, to identify groups of cells with similar profiles.

k-means clustering

This week we look at a classic clustering algorithm called K-means clustering.

K-means is usually described as an algorithm, but we're going to view it from a different perspective: as fitting the data to an implicit probability model. We'll see that the K-means clustering algorithm is equivalent to fitting a probability model called a Gaussian mixture model, with a set of additional simplifying assumptions. These modeling assumptions aren't explicit in how the K-means algorithm is usually described, but if they are violated, K-means clustering can give poor results.

By following the philosophy of specifying a generative probability model of the data first, the implicit assumptions of K-means become explicit. We will see K-means as a special case of a general class of mixture models, where we've made very specific choices for a Gaussian distribution as our model of each individual cluster in the data. We will see that we're free to choose other probability models for clusters. Fitting these models results K-means-like clustering algorithms using expectation maximization, allowing us to cluster datasets where the implicit assumptions of standard K-means do not hold.

notation and definition

We have $N$ data points $X_i$, and we want to assign them to clusters.

Each $X_i$ is a point in a multidimensional space. It has coordinates $X_{iz}$ for each dimension $z$. In two dimensions $(Z=2)$ we can visualize the $X_i$ as dots on a scatter plot. It's easiest to think about K-means clustering in 2D, but important to remember that many applications of it are in high dimensions. For example, gene expression vectors for $G$ different genes in each cell are points in a $G$-dimensional space. For a second example, w-mer frequencies for DNA w-mers of length $W$ in a phage genome are points in a $4^W$-dimensional space.

A cluster is a group of points that are close together, for some definition of "close". One easy definition to imagine is "close in space". The Euclidean distance between any two points $X_i$ and $X_j$ is

$$ d_{ij} = \sqrt{ \sum_z ( X_{iz} - X_{jz} )^2 } $$

Suppose we know there are $K$ clusters. (This is a drawback of K-means: we have to specify $K$.) Suppose we assign each point $X_i$ to a cluster (i.e. a set) $C_k$, so we can refer to the indices $i \in C_k$. We can calculate the centroid of each cluster, $\mu_k$: its mean location, i.e. its center of mass, which we obtain by averaging independently in each dimension $z$:

$$ \mu_{kz} = \frac{ \sum_{i \in C_k} X_{iz} } { \left\vert C_k \right\vert } $$

where the denominator $\left\vert C_k \right\vert$ is the number of points in cluster $k$ : the cardinality of set $C_k$, if you haven't seen that notation before.

The centroid is just another point in the same multidimensional space. We can calculate a distance $d_{ik}$ of any of our items $X_i$ to a centroid $\mu_k$, the same way we calculated the distance between two points $i,j$.

For any given assignment $C$ consisting of $K$ sets $C_k$, we can calculate the $K$ centroids $\mu_k$, and then calculate the distance $d_{ik}$ from each point $X_i$ to its assigned centroid $\mu_k$. We can calculate a total squared distance for a clustering $C$:

$$ \begin{eqnarray} D_{C} & = & \sum_k \sum_{i \in C_k} d_{ik}^2 \ & = & \sum_k \sum_{i \in C_k} \sum_z ( X_{iz} - \mu_{kz} )^2 \ \end{eqnarray} $$

A K-means clustering of the data is defined by finding a clustering $C$ that minimizes the total squared distance $D_C$, given $K$. Why squared distance? Why doesn't it just minimize the sum of the distances? We'll see. We literally try to place $K$ means (centroids) in the space such that each point $X_i$ is close to one of them. That's the definition of a K-means clustering. Now, how do we find one?

algorithm

We start with some randomly chosen centroids $\mu_k$. Then iterate:

• Assignment step: Assign each data point $X_i$ to its closest centroid $\mu_k$.

• Update step: Calculate new centroids $\mu_k$.

Iterate until the assignments don't change. Does this algorithm look familiar? Hrmmm.

It is possible for a centroid to have no points assigned to it, so you have to do something to avoid dividing by zero in the update step. One common thing to do is to leave such a centroid unchanged.

The algorithm is guaranteed to converge, albeit to a local rather than a global optimum. The k-means algorithm is sometimes also called Lloyd's algorithm.

local minima; initialization strategies

K-means is extremely prone to spurious local optima. For instance, you can have perfectly obvious clusters yet end up with multiple centroids on one cluster and none on another.

People take two main approaches to this problem. They try to choose the initial guessed centroid locations "wisely", and they run K-means many times and take the best solution (best being the clustering that gives the lowest total distance $D_C$).

Various ways of initializing the centroids include:

• choose $K$ random points in space;
• choose $K$ random points from $X$ and put the initial centroids there;
• assign all points in $X$ randomly to clusters $C_k$, then calculate centroids of these.

soft k-means variant

Standard K-means is distinguished by a hard assignment: data point $i$ belongs to cluster $k$, and no other cluster. We can also imagine doing a soft assignment, where we assign a probability that point $i$ belongs to each cluster $k$.

Let's introduce $A_i$, the assignment of point $i$, so we can talk about $P(A_i=k \mid X_i, \mu)$: the probability that we assign point $X_i$ to cluster $k$ given the K-means centroids $\mu = \mu_1..\mu_K$.

What should this probability be, since we haven't described K-means in probabilistic terms? (Not yet, anyway.) The standard definition of soft k-means calculates a "responsibility" $r_{ik}$:

$$ r_{ik} = \frac {\exp \left( -\beta d_{ik}^2 \right) } {\sum_{k'} \exp \left( -\beta d_{ik'}^2 \right) } $$

where $\sum_k r_{ik} = 1$ for each point $i$, since the denominator forces normalization. We call it a "responsibility" instead of a probability because we haven't given it any well-motivated justification (again, not yet).

People call the $\beta$ parameter the stiffness. The higher $\beta$ is, the closer a centroid $k$ has to be to a point $i$ to get any responsibility $r_{ik}$ for it. In the limit of $\beta \rightarrow \infty$, the closest centroid gets $r_{ik} = 1$, and we get standard K-means hard clustering as a special case.

The centroid of each cluster $k$ is now a weighted mean, with each point $X_i$ weighted by its responsibility (remember that each point is a vector; we're going to drop the indexing on its dimensions, for more compact notation):

$$ \mu_k = \frac { \sum_i r_{ik} X_i} { \sum_i r_{ik} } $$

The soft K-means algorithm starts from an initial guess of the $\mu_k$ centroids and iterates:

• Assignment step: Calculate responsibilities $r_{ik}$ for each data point $X_i$, given the current centroids $\mu_k$.

• Update step: Calculate new centroids $\mu_k$, given responsibilities $r_{ik}$.

Fine, but this "responsibility" business looks ad hoc. Is there a justification for what we're doing?

mixture models

A mixture model is a generative probability model composed of other probability distributions. A mixture model is specified by:

• $Q$ components.
• each component has a mixture coefficient $\pi_q$, the probability of sampling each component.
• each component has its own parameters $\theta_q$, and generates a data sample $x$ with some probability $P(x \mid \theta_q)$.

The probability of sampling (generating) an observed data point $x$ goes through two steps:

• sample a component $q$ according to its mixture coefficient $\pi_q$
• sample data point $x$ from the component $q$'s probability distribution $P(x \mid \theta_q)$.

This is a simple example of a hierarchical model. More complicated hierarchical models have more steps. It's also a simple example of a Bayesian network composed of two random variables, with an random variable for the observed data dependent on a hidden random variable for the component choice.

The probability that an observed data point $x$ is generated by a mixture model is the marginal sum over the unknown component $q$:

$$ P(x \mid \theta) = \sum_q \pi_q P(x \mid \theta_q) $$

If we had to infer which (hidden) component $q$ generated observed data point $x$, we can calculate the posterior probability:

$$ P(q \mid x) = \frac{\pi_q P(x \mid \theta_q)} { \sum_{q'} \pi_{q'} P(x \mid \theta_{q'})} $$

The mean (average) over many data points $X_i$ assigned to a mixture is, for each component $q$:

$$ \mu_q = \frac{\sum_i P(q \mid X_i) \; X_i} {\sum_i P(q \mid X_i)} $$

You can see this is the update step of soft K-means, with a probability $P(q \mid X_i)$ in place of the ad hoc responsibility $r_{ik}$. But there's a missing piece: we haven't said anything yet about what the component probability distributions $P(x \mid \theta_q)$ can be.

That's because the components $P(x \mid \theta_q)$ can be anything you like. It's most common to make them all the same elemental type of distribution. So we can have mixture exponential distributions with parameters $\lambda_q$; we can have mixture Poisson distributions also with parameters $\lambda_q$; we can have mixture multinomial distributions with parameters $p_q$; and so on.

Probably the most common mixture model is a mixture Gaussian distribution, with parameters $\mu_q$ and $\sigma_q$ for each component. This might arise in trying to fit data that had multiple modes (peaks), with different peak widths, and different proportions of data in each peak. A mixture Gaussian in a single dimension would give:

$$ P(x,q \mid \theta) = \pi_q \left( \frac{1}{\sqrt{2\pi\sigma_q^2}} \exp \left( \frac{-(x-\mu_q)^2}{2\sigma_q^2} \right) \right) $$

We could use a two-component mixture Gaussian to specify a bimodal distribution for a real-valued random variable $X$, for example.

soft K-means as a mixture probability model

Let's stare at the mixture Gaussian model for a while, and compare it to soft K-means. Specifically, consider what the posterior probability $P(q \mid X_i, \theta)$ looks like for a multidimensional mixture Gaussian, compared to the responsibility $r_{ik}$ calculation.

First notice that the $(x - \mu_q)^2$ term in the one-dimensional Gaussian looks sort of like it's paralleling the $d_{iq}^2$ term in the multidimensional k-means responsibility. Turns out there's an especially simple multidimensional generalization of the Gaussian, a spherical Gaussian, where we replace a one-dimensional distance $(x - \mu)$ from the mean with the multidimensional distance $d_{iq}$. A spherical Gaussian is still controlled by a single variance parameter $\sigma^2$; its probability density falls off symmetrically in all directions from its mean. (More general multidimensional Gaussian distributions allow different variances in each dimension, and correlations between dimensions.)

So how about the $\sigma_q$ for each different spherical Gaussian component, where are they in the responsibility? A mixture Gaussian requires that we specify a variance $\sigma_q^2$ for each component $q$, and no such component-dependent term appeared in soft K-means. So in additional to assuming spherical Gaussian components, let's go a step further, and assume that there is a single constant $\sigma = \sigma_q$ for all spherical Gaussian components $q$.

Let's also go yet another step further, and assume that all components are equiprobable: $\pi_q = \frac{1}{Q}$.

Now you should be able to prove to yourself that after making these assumptions, the mixture Gaussian posterior probability equation reduces to:

$$ P(q \mid X_i, \theta) = \frac{ \exp \left( \frac{-d_{iq}^2}{2\sigma^2} \right)} { \sum_{q'} \exp \left( \frac{-d_{iq'}^2}{2\sigma^2} \right)} $$

As if you haven't already recognized the equation for the responsibilities $r_{ik}$ in soft K-means, let's go ahead and define a stiffness $\beta = \frac{1}{2\sigma^2}$, and:

$$ P(q \mid X_i, \theta) = \frac{ \exp \left( -\beta d_{iq}^2 \right)} { \sum_{q'} \exp \left( -\beta d_{iq'}^2 \right)} $$

implicit assumptions of K-means

Having derived the responsibility update equation for soft K-means from first principles, we've laid bare its implicit assumptions:

• the data are drawn from a mixture Gaussian distribution;
• composed of spherical Gaussians;
• each component has an identical spherical Gaussian variance $\sigma$ -- each component is the same "width"; and
• each component has an equal expected number of data points.

It should not be surprising that K-means may tend to fail when any of these assumptions is violated. Textbook descriptions of K-means may tell you it can fail when the individual data clusters are asymmetrically distributed, have different variances, or have different sizes in terms of number of assigned data points — but they will typically not tell you why.

fitting mixture models with expectation maximization

You've probably already realized that soft K-means, when viewed as a probability model, is another example of an expectation maximization (EM) algorithm. Expectation maximization is a common way of fitting mixture models, and indeed other models with hidden variables.

Here's how you'd use expectation maximization to fit a mixture Gaussian model to data. To simplify things just for the sake of this description, let's assume that there is a single known, fixed variance parameter $\sigma$, as in a soft K-means stiffness. But let's relax one of the other K-means assumptions, and allow different mixture coefficients $\pi_q$. Then, starting from an initial guess at the means $\mu_q$:

• Expectation step: Calculate posterior probabilities $P(q \mid X_i, \mu, \sigma, \pi)$ for each data point $X_i$, given the current means (centroids) $\mu_q$, fixed $\sigma$, and mixture coefficients $\pi_q$.

• Maximization step: Calculate new centroids $\mu_q$ and mixture coefficients $\pi_q$ given the posterior probabilities $P(q \mid X_i, \mu, \sigma, \pi)$.

We can follow the total log likelihood $\log P(X \mid \theta)$ as we iterate, and watch it increase and asymptote. When we start from different starting conditions, a better solution has a better total log likelihood.

When we calculate the updated mixture coefficients $\pi_q$, that's just the expected fraction of data points assigned to component $q$:

$$ \hat{\pi}_q = \frac{\sum_i P(q \mid \cdot) } {N} $$

If we had to fit more than just a mean parameter $\mu_q$ for each component, we would have some way of doing maximum likelihood parameter estimation given posterior-weighted observations. For example, if we were also trying to estimate $\sigma_q$ terms, we could calculate the expected variance for each component $q$, not just the expected mean.

probability models of count data

Let's just first recognize that RNA-seq count data are not Gaussian-distributed. Counts aren't real-valued, and they can't be negative. If we're going to apply k-means to an scRNA-seq data set, we have no right to expect it to work, unless we can convince ourselves that the Gaussian is a decent approximation (and it's not). Let's think about how we want to model RNA-seq count data.

If an RNA-seq experiment generated observed counts from a mean expression level like pulling balls out of urns, then the differences we see across replicates of the same condition would just due to finite count sampling error. We would expect the observed counts $y_{ig}$ across several replicates $i$ to be Poisson-distributed around a mean $\mu_{ig}$.

The Poisson distribution only has one parameter. The variance of the Poisson is equal to its mean $\mu$. This is a strong assumption about the variance: that it's only accounting for Poisson sampling noise.

In real biological data the counts $y_{ig}$ in replicates - biological replicates, or even just technical replicates - have more variance than the Poisson predicts. They are overdispersed. This isn't surprising. If the samples are outbred organisms with different genotypes, for example, we get expression variation across individuals due to genotype variation. We also get variation from all the host of other environmental and experimental factors that are changing when we do biological replicates. When the sample $i$ is a single cell from a scRNA-seq experiment, not a biological replicate of a bulk RNA-seq experiment, we get additional variance from cell-to-cell variation for all sorts of biological reasons.

If only as a practical matter, when we make probability models of RNA-seq count data, we want to use a form of distribution that allows us to control the variance separately from the mean, so we can model this overdispersion. We need at least a two-parameter distribution.

two typical distributions used for RNA-seq counts

Empirically, two different distributions have been seen to fit RNA-seq count data reasonably well: the negative binomial distribution and the lognormal distribution. Both distributions are controlled by two parameters, not just one, allowing the variance to be controlled separately from the mean. Both are "fat-tailed" distributions that roughly match the sort of variation we empirically see across replicates in real RNA-seq count data.

The lognormal distribution tends to arise in processes with multiplicative noise, as opposed to additive noise. Additive noise tends to lead to normal (Gaussian) distributions, because the distribution for the mean of a sum of independent samples converges a Gaussian in the limit of many samples (this is the central limit theorem). Multiplicative noise is the same as saying as additive noise in log space, leading to lognormal distributions. In gene expression, it's easy to imagine that the observed variation in expression levels arises from multiplicative biological noise: we use the language of "two-fold" expression differences, for example, speaking in fold change (multiplicative) terms.

Many data analytic methods either explicitly or implicitly assume that a "sampling error" (i.e. differences from the expected mean; also called a "residual") is normally distributed. When the data are actually lognormally distributed, an easy hack is to log-transform the data before analyzing it with such a method. For example, we can analyze a matrix of $\log y_{ig}$ instead of the original $y_{ig}$. This corresponds to assuming a lognormal distribution for the data, while using a method that assumes normality.

The lognormal distribution seems like a bit of a hack though. It can't be exactly the right distribution to use for count data. Our count data $y$ are discrete integers for $y \geq 0$. The lognormal distribution is continuous, generating real-valued samples on the open interval $(0, \infty)$, undefined at $y=0$. We can expect trouble and/or fiddly bits in trying to apply lognormal distributions to count data with zeros in it.

The alternative, the negative binomial distribution, has the advantage of being a discrete distribution on $y = [0,\infty)$, automatically making it more appropriate for count data. The negative binomial is widely used in RNA-seq analyses as the probability model for counts, and the homework this week is based on the negative binomial distribution. Did the field just pull this distribution out of the air, as an arbitrary choice?

Well, yeah, I sort of think it did. But as with many things we're seeing in the course, a reasonable ad hoc approach often leads to a deeper probabilistic understanding.

start from a mixed Poisson model

Let's assume that there is a true expected count $\mu_{ig}$ parameter for transcript $g$ in replicates $i$ of the same cell population or single cell of the same type. We would normally talk about expression levels in terms of normalized relative abundances $\tau$ in TPM, or nucleotide abundances $\nu$. Working in counts simplifies some notational details here. If we have $N$ total mapped read counts, $\mu_{ig} = N \nu_{ig} = E(c_{ig})$, where $E(c_{ig})$ means the expected mean counts.

Moreover, let's only worry about one expected count value $\mu$ at a time, and drop the $i$ and $g$ subscripts in the notation. The same process will apply independently to each sample $i$ and each gene $g$.

In our observed data, we observe mapped read counts $y$. If every sample has an identical expected count $\mu$, we expect $y$ to be Poisson-distributed with mean $\lambda = \mu$.

However, we want the expected counts in each sample to itself be subject to variance across samples, for both biological and technical reasons. Each time we do a replicate or look at a single cell, the expression level in the sample is not an exact replicate of another sample that we tried to process identically, or a single cell of the same cell type. So we want to introduce an additional step in our generative model that says that each sample has its own expected count $\lambda$, which is sampled around the overall expected count $\mu$.

This leads to a two-step generative model:

$$ P(y \mid \mu) = \int_{\lambda} P(y \mid \lambda) P(\lambda \mid \mu) d\lambda. $$

The $P(y \mid \lambda)$ term will be a Poisson PDF. We haven't said what the $P(\lambda \mid \mu)$ term is yet. We'll choose this distribution to describe what we think the variation in $\lambda$ from sample to sample looks like.

The overall model of "generate a $\lambda$ parameter, then generate Poisson-distributed counts $y$ from the $\lambda$" is just another kind of mixture model. This one is typically called a "mixed Poisson" model, where the Poisson's mean parameter $\lambda$ isn't fixed, but instead is varying according to some other distribution $P(\lambda)$.

Any mixed Poisson model has more variance than the Poisson alone. If we paid attention in statistics class, the "law of total variance" told us that $\mathrm{Var}(y) = E \left[ \mathrm{Var}(y\mid\lambda) \right] + \mathrm{Var} \left[E(y \mid \lambda)\right]$. The first term is the variance of the Poisson. The second term is the variance of the expected mean of the Poisson, which here is the variance of $\lambda$.

OK. Now let's now state that we intend to use a single parameter, called $\phi$, to control the overdispersion of our data relative to a simple Poisson. We'll call $\phi$ the dispersion parameter.

By convention, people define $\phi$ by reference to the "coefficient of variation" (CV) of $\lambda$, rather than directly parameterizing the variance of $\lambda$. A CV is the standard deviation normalized to the mean: CV = $\frac{\sigma}{\mu}$ for standard deviation $\sigma$ and mean $\mu$. We choose to define $\phi$ by $\sqrt{\phi} = \frac{\sigma}{\mu}$, which means the variance of lambda is $\sigma^2 = \phi \mu^2$.

I'm sure that was confusing. Let's restate more simply as a bottom line result.

The variance of our counts $y$ is overdispersed relative to the Poisson, such that:

$$ \sigma_y^2 = \mu + \phi \mu^2. $$

The first term $\mu$ is from Poisson variance alone. The second term $\phi \mu^2$ is from the additional variance from a distribution for $P(\lambda \mid \mu)$ that we haven't stated yet. If $\phi=0$, there's no overdispersion, and there is no variation in the $\lambda$ that feeds into the Poisson; the counts then are just Poisson-distributed with mean $\mu$ and variance $\mu$.

Whatever we say that distribution $P(\lambda \mid \mu)$ is, we intend to control it with two parameters: expected mean count $\mu \geq 0$, and a dispersion $\phi \geq 0$.

We can choose any continuous distribution on $[0, \infty)$ for our model of $P(\lambda \mid \mu)$. Common choices include a gamma distribution, a so-called "inverse Gaussian" distribution, or a lognormal distribution (although the lognormal can't generate $\lambda=0$).

Let's semi-arbitrarily choose the gamma distribution. Now we have to figure out how to parameterize a gamma distribution with our $\mu$ and $\phi$ parameters.

the Gamma-Poisson distribution

A gamma distribution is defined in terms of two parameters $k > 0$ and $\theta > 0$. A gamma distribution typically arises as a sum of $k$ independent exponential random variables, each with the same waiting time $\theta$. For example, if the expected mean waiting time between radioactive decay events is $\theta$ seconds (or equivalently, the rate of decay is $\frac{1}{\theta}$ per second), then the expected time $t$ it takes to observe $k$ decay events is distributed $t \sim \mathrm{gamma}(k, \theta)$. For $k=1$, the gamma distribution becomes an exponential distribution.

The mean of the gamma is $k \theta$. The variance is $k \theta^2$.

We don't need to worry about the PDF of the gamma or anything like that. The mean and variance are sufficient for us to figure out the appropriate change of variables so we can parameterize the gamma distribution by our $\mu$ and $\phi$. We set mean $\mu = k \theta$ and variance $\phi \mu^2 = k \theta^2$, and solve:

$$ \begin{eqnarray} k & = & \frac{1}{\phi} \ \theta & = & \mu \phi \end{eqnarray} $$

Now we know enough to sample counts from our proposed two-step process, given parameters $\mu$ and $\phi$:

1. Sample $\lambda \sim \textrm{gamma}(k = \frac{1}{\phi}, \theta = \mu \phi)$
2. Sample $y \sim \textrm{Poisson}(\lambda)$.

We could use NumPy routines rng.gamma(shape=k, scale=$\theta$) and rng.poisson(lam=$\lambda$) to implement this sampling.

When we substituting the Poisson PDF for $P(y \mid \lambda)$ and the gamma PDF for $P(\lambda \mid \mu, \phi)$, the mixed Poisson integral

$$ P(y \mid \mu, \phi) = \int_{\lambda} P(y \mid \lambda) P(\lambda \mid \mu, \phi) d\lambda $$

turns out to have a closed form solution:

$$ P(y \mid \mu, \phi) = \frac{\Gamma \left( y + \phi^{-1} \right)} { \Gamma (\phi^{-1}) \; \Gamma (y+1)} \left( \frac{1}{1 + \mu \phi} \right)^{\phi^{-1}} \left( \frac{\mu }{\phi^{-1} + \mu} \right)^y $$

OK... but yow.

This is the discrete PMF for the Gamma-Poisson distribution. The Gamma-Poisson is a specific type of mixed Poisson distribution where we've chosen to use a gamma distribution to specify the uncertainty over the mean parameter $\lambda$ for the Poisson.

If you haven't seen that notation $\Gamma(x)$ before, that's the Gamma function. Not to be confused with a gamma distribution. The Gamma function is just the real-valued generalization of the factorial, with an off-by-one issue. For an integer $n$,

$$ \Gamma(n) = (n-1)! $$

So that leading term actually looks a lot like a binomial coefficient.

So, we want to use a Gamma-Poisson model for our count data. We sure hope there's convenient Python routines for numerically computing this PDF (or log PDF), say in scipy.stats... right? right? Nope. Not there. How about in Wikipedia? There's a page for the Gamma-Poisson, but it redirects to... a distribution called the negative binomial distribution. Now we have to see what's up with that.

the negative binomial distribution

What's up with that is that the Gamma-Poisson distribution and the negative binomial distribution are the same thing, albeit arrived at by different routes and described with different parameterization. Since SciPy provides routines for the negative binomial distribution, we'll have to figure out another change of variables now, to get our parameters $\mu$ and $\phi$ into whatever SciPy needs to make these function calls work.

The negative binomial arises when we have some sort of random discrete event where we can talk about a probability $p$ of success and $1-p$ of failure. (Each event is called a Bernoulli trial, in the jargon.) What's the probability of obtaining $k$ failures before reaching exactly $n$ successes in a sequence of Bernoulli trials (where $n$ is pre-specified)? If $k=1$, this is just a geometric distribution. More generally for $k \geq 1$, we get the negative binomial distribution.

We know the chain ends in a success because we stop when we reach the $n$'th success. The remaining $n-1$ successes and $k$ failures can occur in any order (any permutation). So:

$$ \begin{eqnarray} P(k \mid n, p) & = & p \cdot { k + n - 1 \choose n-1 } p^{n-1} (1-p)^k \ & = & { k + n - 1 \choose n-1 } p^n (1-p)^k \ \end{eqnarray} $$

Voila, the PMF for the negative binomial distribution.

aside: why negative binomial?

The name is totally confusing. The binomial distribution arises when we're counting the total number of successes $k$ in a fixed number of Bernoulli trials $n$: the total number of trials is fixed, the number of failures $n-k$ varies. This is not really the same sort of question as counting the total number of failures $k$ in a series of Bernoulli trials that ends with the $n$'th success, where it's the number of successes that's fixed and the total number of trials $n+k$ varies. So the name doesn't really come from any particularly useful parallel between the binomial and the negative binomial distributions.

The name actually comes from a way of manipulating/rearranging the binomial coefficient ${k + n - 1 \choose n-1}$ in the PMF equation above. It can be rewritten as:

$$ = \frac{(n + k - 1) ( n + k - 2) \ldots (n+1)(n)}{ k! } $$

and if I'm being silly, I can rewrite that by pulling a -1 out of each term in the numerator, then reversing the order of those terms:

$$ = (-1)^k \frac{ (-n)(-n-1) \ldots (-n - k + 2) (-n - k - 1)}{ k! } $$

and then I can abuse binomial coefficient notation by rewriting this in terms of a "negative" binomial coefficient:

$$ = (-1)^k { -n \choose k} $$

Thus Moriarty would correctly but evilly write the negative binomial PMF as:

$$ P(k \mid n, p) = (-1)^k { -n \choose k } p^n (1-p)^k $$

But the only reason to write it that way is to see why people call it a "negative binomial" distribution.

never mind all that, what we need to do is...

In SciPy, the scipy.stats.nbinom.pmf(k,n,p) and scipy.stats.nbinom.logpmf(k,n,p)() functions calculate the PMF and log PMF of the negative binomial. The PMFs for the Gamma-Poisson and the negative binomial are identical except for a change of variables, and for generalizing $n$ to be real-valued in the Gamma-Poisson by using gamma functions instead of factorials.The SciPy negative binomial functions accept real-valued n, so they can be used to do calculation the Gamma-Poisson too. You will want to use these SciPy function calls to calculate the log PMF of your observed count data in the pset, for the negative binomial components of your negative binomial mixture distribution.

We want to use mean $\mu$ and dispersion $\phi$ as parameters for a Gamma-Poisson. To get from $\mu, \phi$ to parameters to the negative binomial that we can plug into SciPy, we have:

$$ \begin{eqnarray} p & = \frac{1}{1 + \mu \phi} \ n & = \frac{1}{\phi} \ \end{eqnarray} $$

Note that $(1-p) = \frac{\mu \phi}{1 + \mu \phi}$, which I can divide through by $\phi$ to get $\frac{\mu}{\phi^{-1} + \mu}$, matching the notation used for the Gamma-Poisson.

Once we assume the negative binomial/Gamma-Poisson, then for each gene $g$, we need two parameters to calculate a likelihood of its counts $y_{ig}$ in a sample $i$: its mean number of counts $\mu_g$, and its dispersion $\phi_g$.

Many RNA-seq analysis methods assume a common dispersion across all genes: fitting one $\phi$ for all genes, instead of $G$ different gene-specific $\phi_g$.

Finally! We have our overdispersed count distribution $P(y \mid \mu, \phi)$. The RNA-seq literature almost always calls it a negative binomial distribution, but probabilistically, it seems more intuitive to see it arise as a Gamma-Poisson.

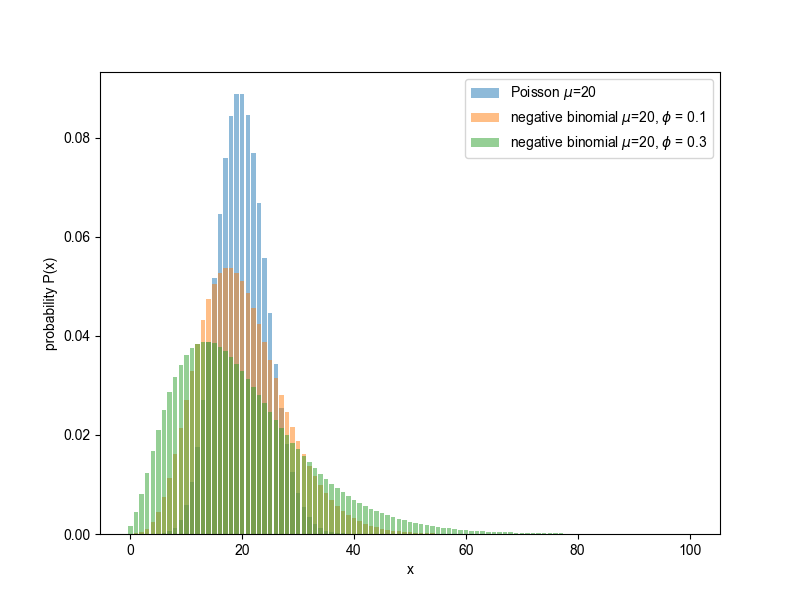Examples of the negative binomial distribution, compared to the Poisson. ('open image in new tab' to embiggen.)

fitting the negative binomial distribution to data

Suppose I give you a bunch of samples $y$ that have been sampled from a negative binomial distribution with unknown parameters $\mu, \phi$. How do I estimate optimal parameter values?

Maximum likelihood fitting of an NB turns out to be a bit fiddly. For almost all practical uses, an alternative parameter estimation strategy suffices, and it's a strategy worth knowing about in general: method of moments (MOM) estimation.

The idea is that since I know the relationship between the NB parameters and the mean and variance (in the limit of having lots of observed data):

$$ \begin{eqnarray} \text{sample mean } \bar{x} & \simeq & \mu \ \text{sample variance } s^2 & \simeq & \mu + \phi \mu^2 \ \end{eqnarray} $$

so why not calculate the mean and variance of the data, then just solve for the parameters:

$$ \begin{eqnarray} \mu^{\mathrm{MOM}} & = & \bar{x} \ \phi^{\mathrm{MOM}} & = & \frac{s^2 - \bar{x}} {\bar{x}^2} \end{eqnarray} $$

We can often get away with MOM estimation. In the homework, you can. Even easier, you don't even need to estimate $\phi$, because I give it to you as a fixed parameter. You only need to estimate the $\mu$ parameter of the NB - which is simply and intuitively just the sample mean of the count data, thankfully.